Welcome to Group Actions on Curves project
Group Actions on Algebraic Curves GAAC
There is a variety of groups that can act on a Riemann surface/algebraic curve over \(\mathbb{C}\); the automorphism group, the mapping class group (here we might allow punctures) and if the curve is defined over \(\bar{\mathbb{Q}}\) the absolute Galois group \(\mathrm{Gal}(\bar{\mathbb{Q}}/\mathbb{Q})\) is also acting on the curve. Understanding the above groups is a difficult problem and these actions provide information on both the curve and the group itself. For all the groups mentioned above, the action can often be understood in terms of linear representations, by allowing the group to act on vector spaces and modules related to the curve itself, as the (co)homology groups and section of holomorphic differentials.
Surveys on Automorphisms of Curves
- J. Antoniadis, A. Kontogeorgis Automorphisms of Curves
- A. Broughton, T. Shaska, and A. Wootton On automorphisms of algebraic curves
Greece 2.0 Basic Research Financing Action (Horizontal support of all Sciences) Sub-action 2 Funding Projects in Leading-Edge Sectors.
News
30. October 2025
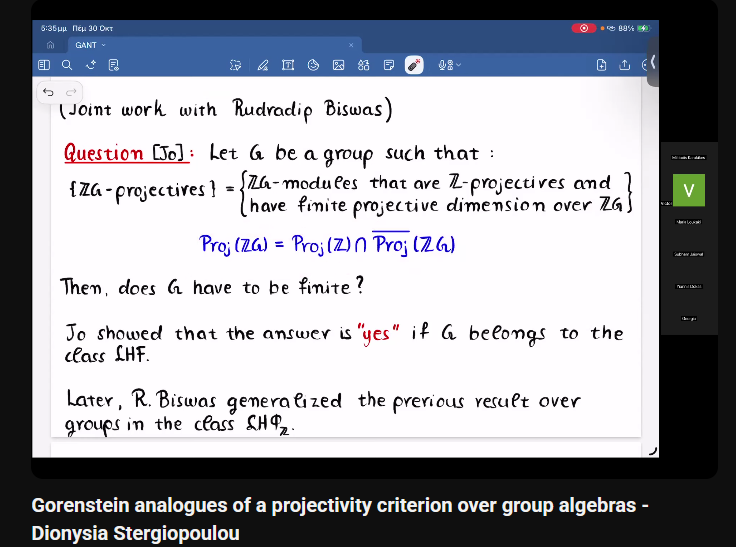
Ομιλία της Διονυσίας Στεργιοπούλου στο online σεμινάριο Greek Algebra and Number Theory
22. July 2025
Ομιλία στο συνέδριο CIMPA Elliptic curves and their applications στο Ινστιτούτο μαθηματικών στην πόλη Γιερεβάν της Αρμενίας

16. June 2025
Παρουσίαση Poster στο συνέδριο Géométrie Algébrique en Liberté στο Ινστιτούτο μαθηματικών της Τουλούζης

23. May 2025
Η ομάδα παρευρέθηκε στο 10ο συνέδριο Άλγεβρας και Θεωρίας Αριθμών, Πανεπιστήμιο Κρήτης, Ηράκλειο

25. April 2025






























